Výpočet obvodu a obsahu pravoúhelníků v praxi (didaktická analýza výuky) | Úvod

Úloha

Kde všude v praxi najdete obvod a obsah?

Úkol pro uživatele: Předtím, než budete pokračovat, odhadněte odpovědi žáků.

Spustit video

Zadání úlohy

Didaktická analýza (DA)

Zaměříme se na didaktickou analýzu obsahu úlohy. Budeme uvažovat ve třech úrovních:

o konceptech oboru (pojmech a jejich vztazích), které nabízí matematika jako východisko řešení úlohy;
o zkušenostech žáků (školních i mimoškolních), které je užitečné při řešení úlohy aktualizovat;
o dlouhodobých cílech, ke kterým výuka směřuje.

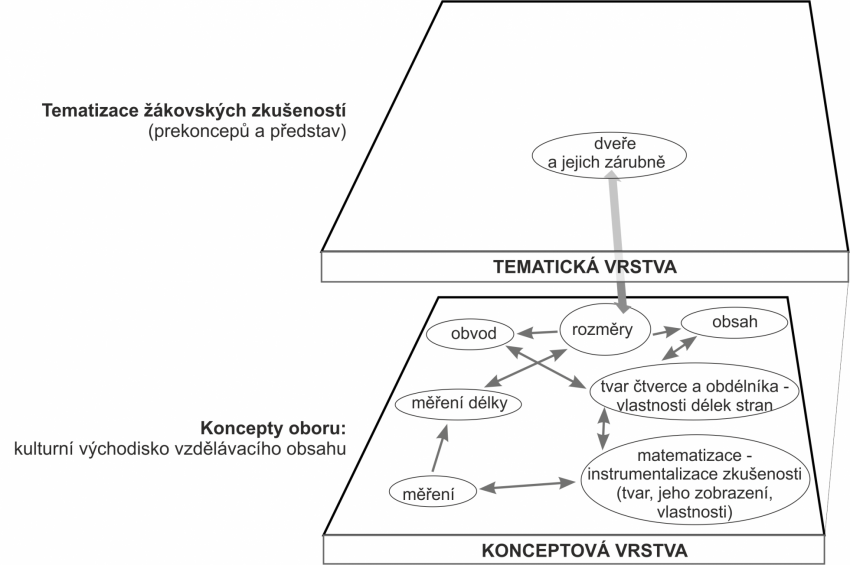
Pro znázornění použijeme konceptový diagram.

Pokračovat

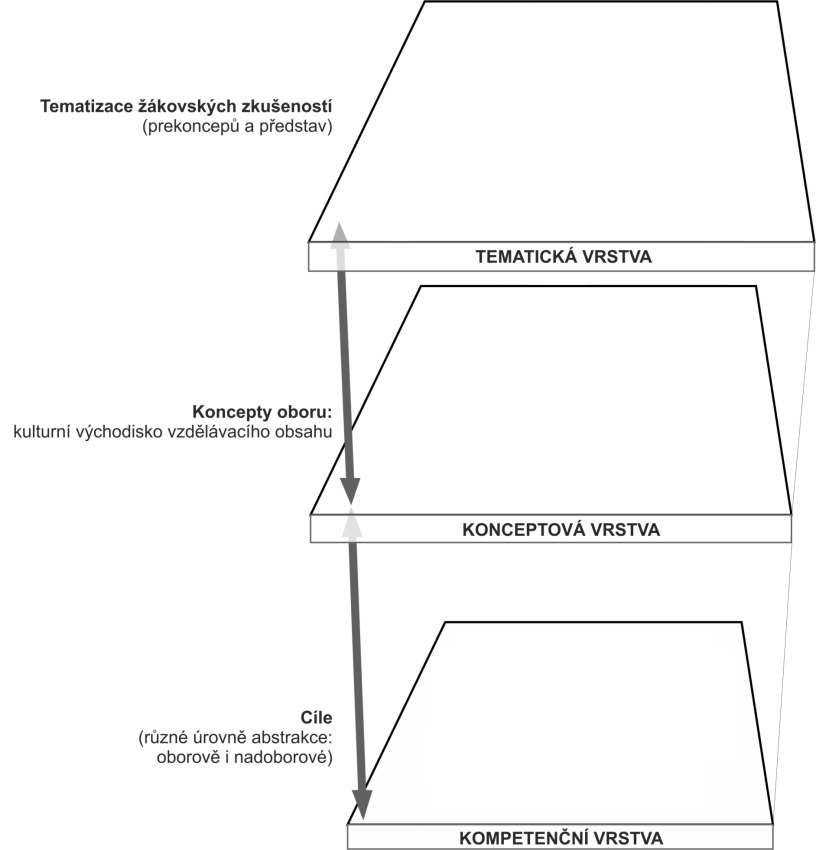
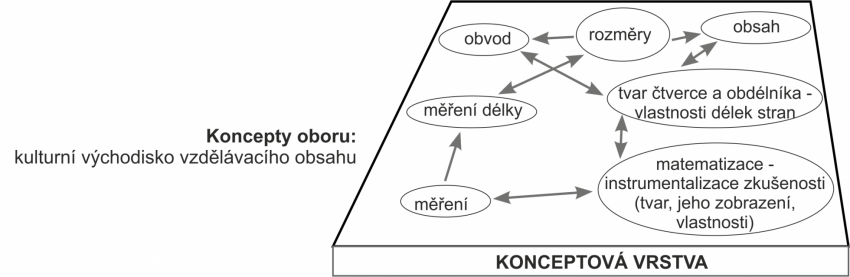
Uvažování o úloze začneme od konceptové vrstvy výuky. Uvědomíme si, které klíčové pojmy mají žáci ve výuce zvládnout, aby porozuměli učivu. V centru jsou pojmy obvod a obsah (co znamenají, jak se vypočítají). S tím souvisí vlastnosti geometrických útvarů, u nichž je zjišťujeme. V případě této výukové situace jsou to čtverec a obdélník a shodnost délek jejich stran. Celá výuková situace souvisí s instrumentalizací zkušeností řešitele úlohy (s matematizací).

Úkol pro uživatele: Které z nabízených pojmů byste zdůraznili? Které byste naopak potlačili?

Doplnili byste do schématu další pojmy? Které?

Pokračovat

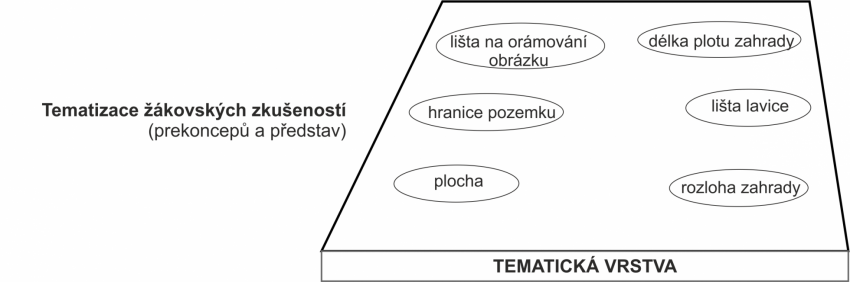
Do tematické vrstvy patří různé žákovy zkušenosti s obvodem a obsahem čtverce a obdélníku jak získané ve škole (řešením rozmanitých obsahově souvisejících úloh), tak mimo školu (řešení problémů vznikajících v životní praxi).

Úkol pro uživatele: Doplnili byste do tematické vrstvy další pojmy?

Pokračovat

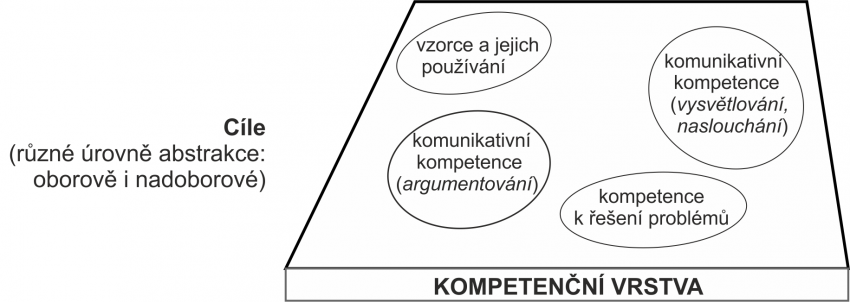
Kompetenční vrstva úlohy zahrnuje dlouhodobé cíle (oborové i nadoborové), k jejichž dosažení může řešení úlohy přispět. Ve schématu jsou uvedeny některé z nich.

Úkol pro uživatele: Doplnili byste do kompetenční vrstvy další cíle?

Pokračovat

Diskuze o řešeních navrhovaných žáky

V další ukázce učitelka diskutuje se žáky řešení úlohy, které si v krátké samostatné práci připravili.

Diskuze je vedena s cílem propojit zkušenosti žáků z běžného života s tím, co se učí ve škole. Prohlubuje se tím porozumění pojmům obvod a obsah. Očekávaný průběh diskuze lze znázornit schématem propojení konceptové a tematické vrstvy. Učitelka vrací pozornost žáků k porozumění základním pojmům (konceptové vrstvě). Žáci reflektují, co znají a jak je jejich poznání využitelné.

Návrhy žáků jsou během diskuze přijímány, upravovány, nebo zavrhovány. Učitelka pomáhá žákům posoudit jejich správnost. Pro porozumění žákovským prekonceptům a představám je důležitý dostatečný čas na evokaci myšlenek a na to, aby žáci dokázali svoje myšlenky zformulovat.

Pokračovat ve videu

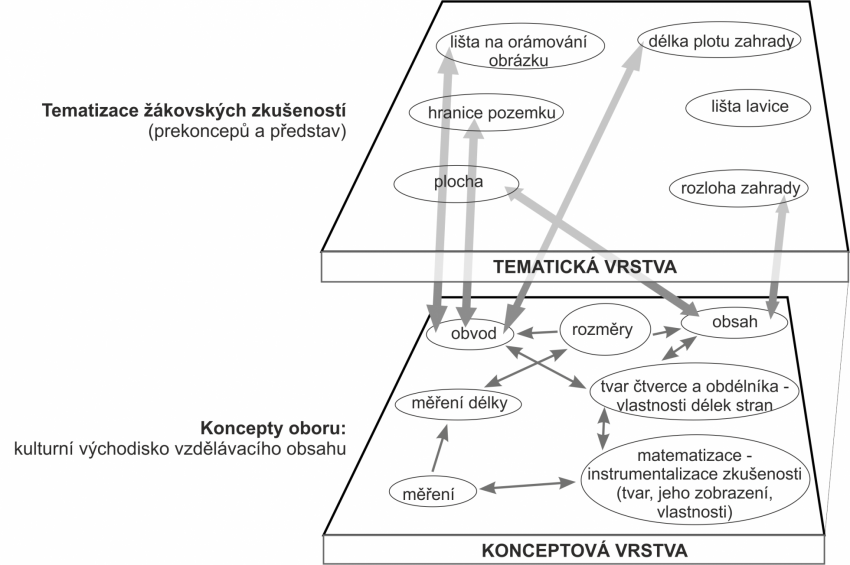
Diskuze o řešeních úlohy navrhovaných žáky

Pokračovat

Konceptový diagram

Organizace diskuze

Řízení diskuze žáků je pro badatelskou výuku klíčovým prvkem. Pro učitele i žáky je zdrojem informací o tom, jak dosud probíhalo učení se jednotlivých žáků, poskytuje důležité informace pro rozhodování o dalších krocích ve výuce.

V diskuzi učitelka poskytuje žákům okamžitou zpětnou vazbu, která slouží k (a) k rozpoznání chybných představ (miskoncepcí) žáků, (b) k nasměrování žáků ke správnému porozumění nebo (c) k vysvětlení nejasného.

Sledujte, jak v pokračování hodiny učitelka diskuzi usměrňuje ve chvíli, kdy žáci navrhnou, že obvod a obsah se používá také při nakupování dveří.

Pokračovat

Konceptový diagram

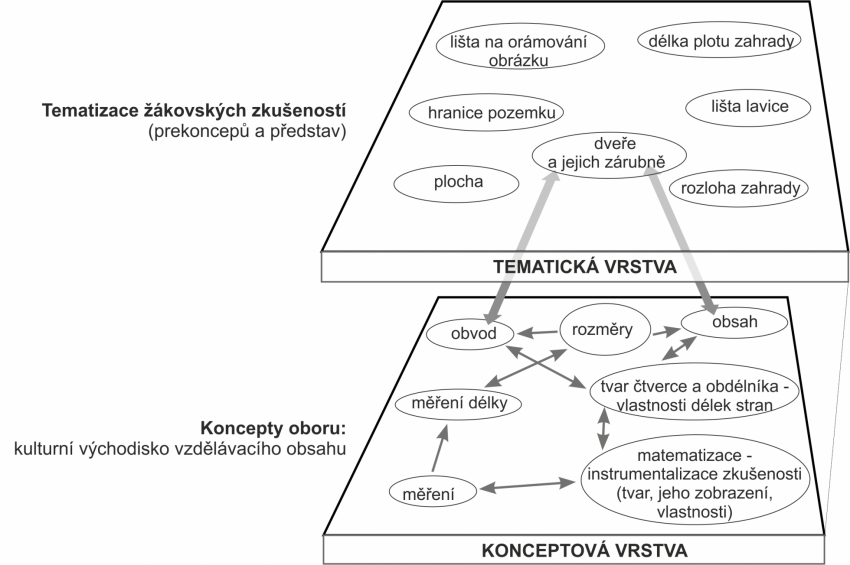
Organizování diskuze žáků

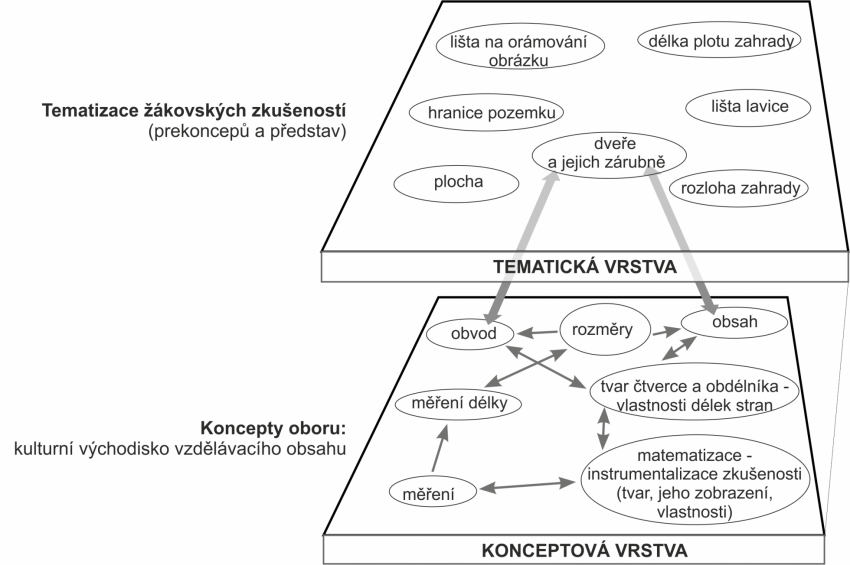
Diskuze

podporuje vzájemné učení. Možnost zpřesňovat a doplňovat odpovědi spolužáků podporuje prohlubování porozumění užívaným pojmům. Žákovský jazyk je tady výhodou. Oceňují ho jak žáci (když mi to říká spolužák, lépe rozumím), tak učitelé (žáci si dovedou poradit a vysvětlit si věci velmi přístupným způsobem).

Při zpřesňování obsahu pojmů se mohou ukázat problémy spojené s tím, že žáci sice pojmu rozumí, ale nedovedou ho používat v jiných kontextech, případně jej nedovedou zařadit mezi pojmy a prekoncepty, kterými již disponují.

Pokračovat

Obvod, obsah, rozměry

Diskuze v předchozí ukázce se točí okolo použití obvodu, obsahu a rozměrů útvaru. Je třeba si uvědomit, že zjištění rozměrů předchází jak určení obvodu, tak i obsahu obrazce. Rozdělení žáků na tři skupiny (obvod, obsah, rozměry) mohlo vytvořit dojem, že se jedná o souřadné pojmy.

Úkol pro uživatele: Promyslete, co musíme znát, aby obdélník či čtverec byl dán jednoznačně (rozměry, obvod, obsah)?

Pokračovat

Porozumění pojmům

Správné používání pojmu předpokládá doplnění porozumění tím, že se žáci vrací k definičním charakteristikám, prozkoumávají správné příklady pojmu a příklady, které daným pojmem nelze označit, a potom znovu vytvářejí a analyzují hypotetická použití pojmu.

V následující ukázce učitelka vede žáky k poznatku, že v mnoha případech v praxi je důležitý tvar předmětu, který je dán jeho rozměry.

Pokračovat ve videu

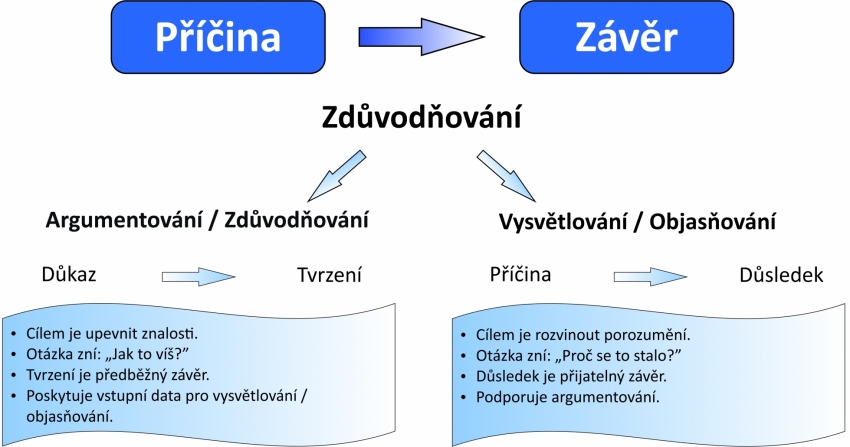
Nová úloha

Žáci řeší novou úlohu (která nebyla v hodině přímo formulovaná): Mohou mít obdélníky, které mají stejný obvod, různý tvar?

Učitelka nabízí různé reprezentace obvodu a obsahu: numerický model, grafický součet úseček pro obvod, které mají žáky podpořit ve formulaci závěru, že obvodem (ani obsahem) rovinného útvaru není dán jeho tvar jednoznačně.

Úkol pro uživatele: Navrhněte další možnosti reprezentace, které by učitel mohl použít, aby žákům ve formulaci závěru pomohl?

Příklady řešení úkolu:

Je např. možné použít provázek, jehož konce svážeme. 4 (3) žáci uchopí provázek na různých místech a natáhnou jej. Tím vymodelují čtyřúhelník (trojúhelník). Jiní 4 (3) žáci dostanou za úkol uchopit provázek na jiných místech, natáhnout jej. Učitel se ptá žáků, co pozorovali.
Žáci dostanou za úkol zakreslit ve čtvercové síti obdélník, jehož obvod je 18 cm. Kolik takových obdélníků je možné nakreslit.
Žáci dostanou za úkol nakreslit ve čtvercové síti čtyřúhelník, jehož obvod je 16 cm.

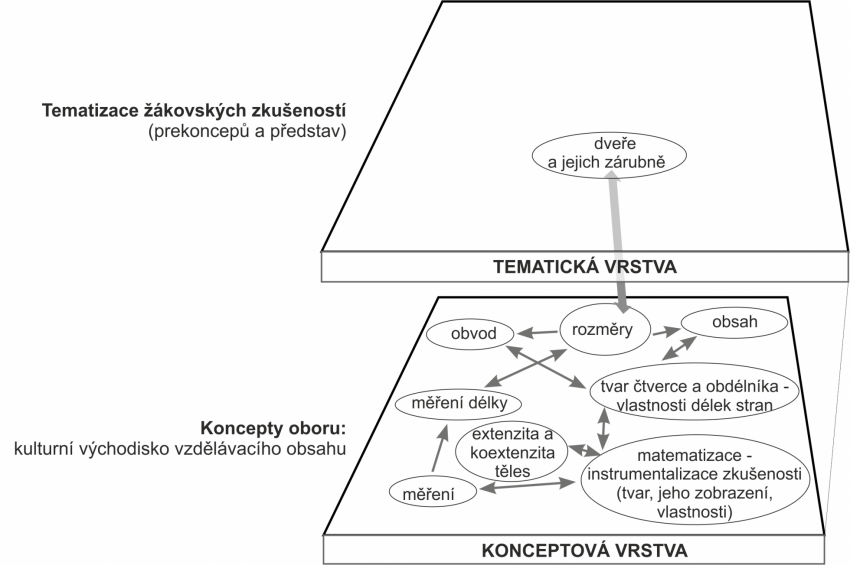
Nový pojem (soumeznost) v konceptové vrstvě

Řešení nové úlohy se opírá o pochopení extenzity (rozlehlosti) a koextenzity (soumeznosti) tělesa. Tyto pojmy si vytvářejí již velmi malé děti, když se při hře pokoušejí vložit tvar (např. krychli, válec, kříž) do odpovídajícího výřezu. Tím získávají přirozenou zkušenost s rozlišováním a tříděním těles podle tvarů. Bez této předběžné zkušenosti by vůbec nemohli začít chápat geometrii. K chápání (ko)extenzity také směřují činnosti s některými pomůckami M. Montessori.

Diskuze, která se ve třídě uskutečnila, se o chápání těchto pojmů opírá. Rozšířili jsme o ně konceptovou vrstvu.

Pokračovat ve videu

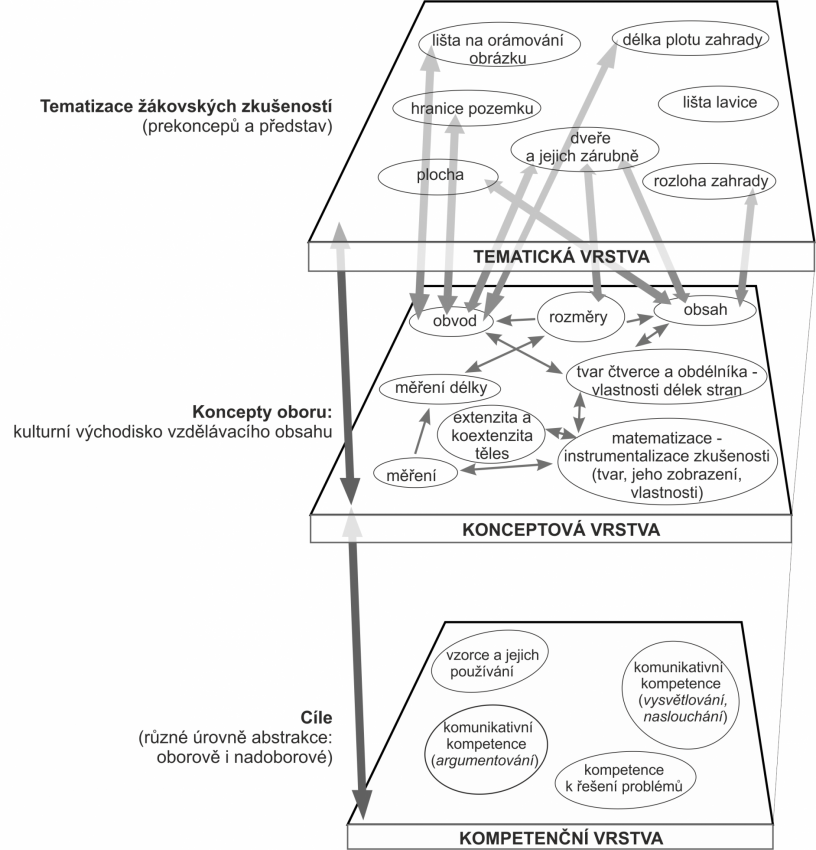
Institucionalizace

V badatelsky orientované výuce je na závěr nutné shrnout, co žáci objevili. Stejně tak v závěru diskuze učitele se třídou je nutné zformulovat závěr. V literatuře se používá termín institucionalizace, který zjednodušeně říká, že závěry diskuze (bádání) označíme jako znalost hodnou zapamatování.

V ukázce ze závěru řešení naší úlohy je vidět, že učitel může i formulování závěrů nechat na žácích.

Jak pokračovat?

K poslední fázi řešení úlohy, institucionalizaci, může napomoci diskuze, při které budeme rozebírat různé možné odpovědi žáků. Podnětem může být komiks (v AJ concept cartoon). Žáci si při diskuzi o tvrzeních jednotlivých dětí v komiksu zpřesňují své vyjadřování i porozumění.

Pokračovat